Number systems
Example: The device shown here counts `smile’s`. The actual count value is `1 0` How many smile´s you have indeed?
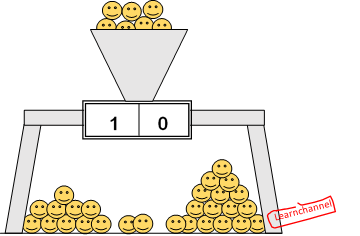
Number systems
- ☺☺☺☺☺ ☺☺☺☺☺
- ☺☺☺☺ ☺☺☺☺ ☺☺☺☺ ☺☺☺☺
- ☺☺
We are used to represent numerical values in the decimal system. But in automation technology the decimal system is - just one of other equivalent number systems.
Characteristics of a number systems
All the number systems used today in have the following in common:
- The digit (for example 0 ....9, 0...f, etc.)
- The base
- The position which takes the digit within the number, determines the valency
In principle how the numerical value is formed, is for all number systems the same. This we want to know for different number systems with different bases.
Decimal system explained
Just an example:
Decimal system explained
The decimal system has the following characteristics:
- Ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- Base: 10
- Value: Powers to the base number 10: 1, 10, 100, 1000, etc.
The representation of the number 205 is actually an abbreviated notation of the sum 200 + 0 + 5 = 205!
Dual system
The functioning of the computer is based on the binary number system. The dual system, in turn, is based on base 2. This also determines the number of digits in the character set of the number system.
- Two digits: 0, 1
- Base: 2
- Value: Powers the base number 2: 1, 2, 4, 8, etc.
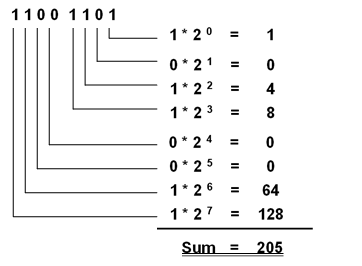
Dual system explained
The example shows that a binary number has greater number of digits than the corresponding decimal number. With 8 digits, binary numbers can be represented values up to 255, with 16 digits up to 65 535.
Hexadecimal system
The Hexadecimal system has the number 16 for its base. As mentioned before, the base determines the number of single digits of the character set - here we have the digits 0 through 9 and the letters A to F.
The hexadecimal system is used to represent with as few digits and characters large numbers. In addition, a conversion of a binary number to hexadecimal number and vice versa is very simple.
- Digit: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
- Base: 16
- Value: Power to the base number 16
Example:
Hexadecimal system
Relation between Dual code and Hexadecimal code:
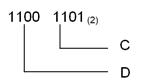
Relation between Dual code and Hexadecimal code
When we compare the binary coded number ‘1100 1101’ with the number in hex ‘CD’, we recognize, that always 4 binary digits build a hex digit. The reason is that with 4 binary numbers exactly 16 numbers can be displayed (from 0 to F).
Example: 1111 1111 1111 1111 Dual in Hex?
Binary coded Decimal (BCD)
The BCD-code converts each digit of a decimal numbers into a binary number and therefore is not another number system. The BCD code is required primarily for inputs and outputs.
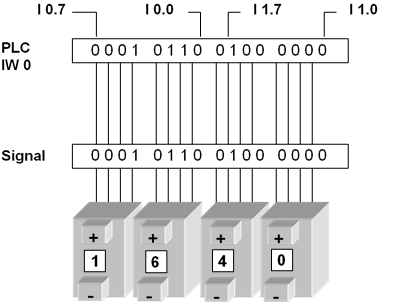
Binary Coded Decimal (BCD)
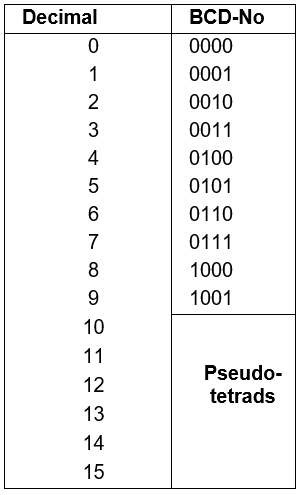
Binary coded Decimal (BCD) - how it is built
This presentation is called Binary Coded Decimal or abbreviated BCD code. The individual digits are encrypted with four binary digits (bits). The representation with 4 bits results from the fact that the most significant decimal digit (910) requires in the binary representation at least 4 digits (1001).
For the presentation of the ten decimal digits 0 through 9 in BCD code the same representation is used as for binary numbers from 0 ... 9.
6 Of the 16 possible combinations with four binary digits the last 6 combination remain unused. We call these combinations "forbidden” and call them pseudo tetrads.