RMS Voltage of a Sinusoidal AC Waveform
Note: RMS stands for `root mean square`
Experiment on the RMS value
An incandescent light bulb is first connected to 50 V AC and then to 50 V DC. You see that the light of the bulb is equally bright in both cases.
Possible explanation: Obviously 50 V AC and 50 V DC has the same power.
Definition and mathematical deduction
The RMS value is the effective value of a varying voltage or current. It is the equivalent steady DC value which gives the same effect.
We want to prove this and find a connection. Since our mains voltage is a sinusoidal voltage, we want to take a closer look at this voltage form:
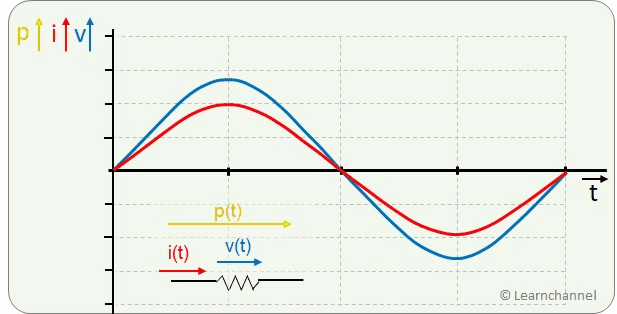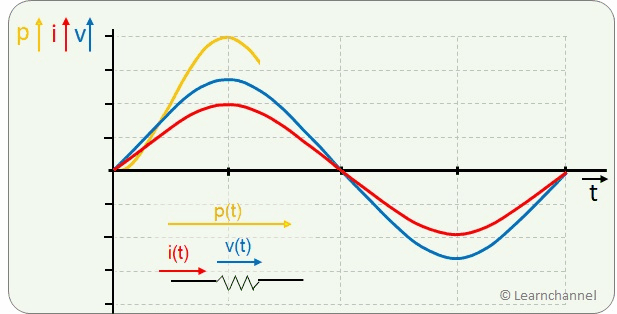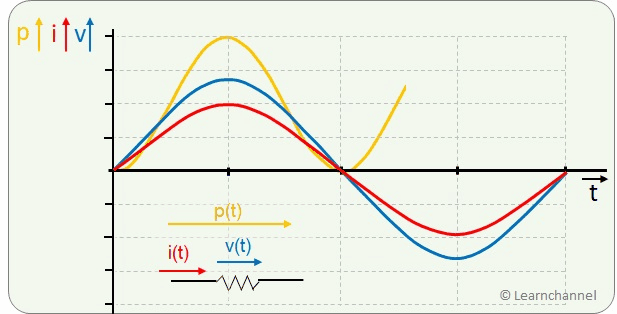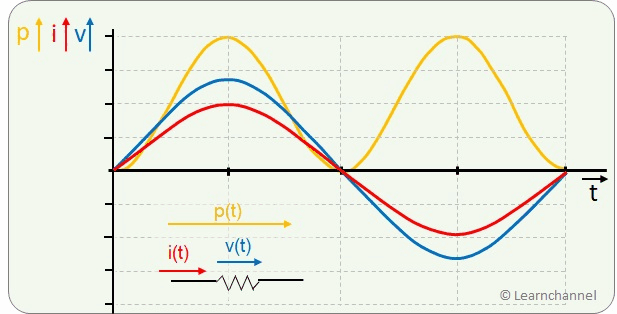
Power of a Sinusoidal AC Waveform
Note: Instantaneous values are usually marked with "small" letters.
The electrical power is the product of voltage and current. In the time diagram, the power at the purely ohmic resistor is always in the positive range with double frequency.
As a user, we are less interested in the instantaneous values, but in the average performance over a certain period of time. We look again at the power curve and apply a few tricks to compare it with the power of a DC voltage:
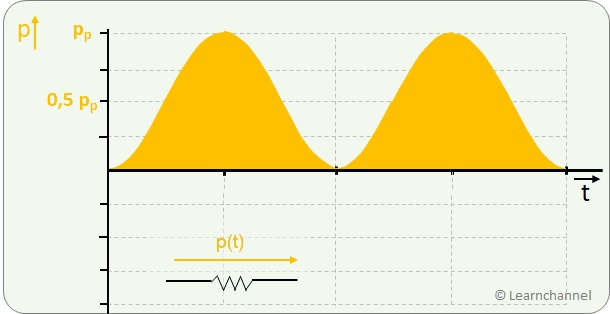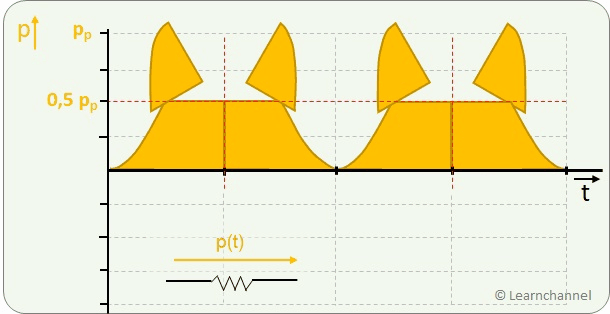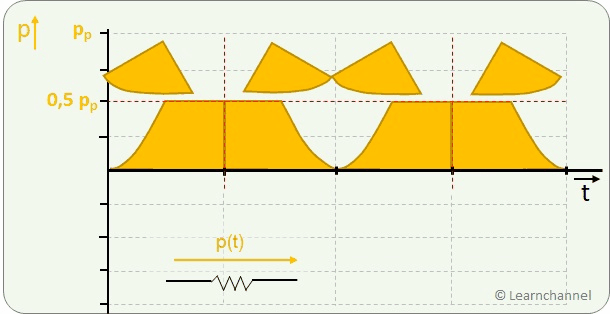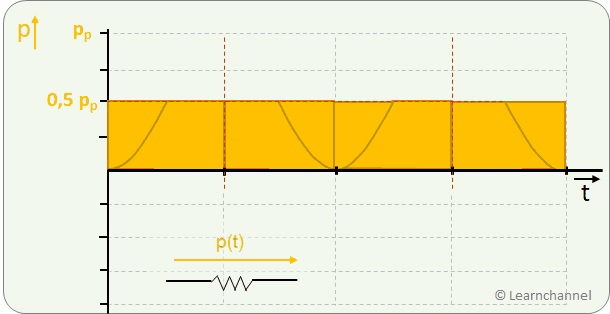
RMS Value of a Sinusoidal AC Waveform
Without much math, let's derive a relationship between the peak value (index 's') and the RMS value:
Formula for RMS value
Note:
Index `p`stands for peak value
√2 is also named as `crest factor`
The RMS value of a continuous-time waveform is the square root of the arithmetic mean of the squares of the values.
It is directly comparable with the DC values of voltage and current, which convert the same electrical power at the ohmic resístance on average over time. The symbols for RMS values are written in upper letters, whereby the index is usually not written.
The factor √2 is called the crest factor.
