English
Deutsch
Português
Español
- Electrical engineering
- Voltage Current Resistance
- Star Delta Transformation
- Practical Voltage and Current Sources, equivalent circuit diagram
- Capacitor to DC voltage
- Inductors in DC Circuits
- Alternating current
- AC Inductive Circuits
- Three-phase Current
- Transformer
- Complex numbers
- Locus Diagram in AC circuits
- Measurement error
- Videos electrical engineering
- Index electrical engineering
Home ⇒ Overview Courses ⇒ Electrical engineering ⇒ Star Delta Transformation
Star Delta Transformation – how it works
The star-delta conversion is a tool for simplifying complex resistor networks. Here, the three resistors are reconnected from delta to star - and vice versa, with correspondingly altered resistance values, so that the ratios between the pins remain the same in both circuit variants.
Delta to Star Transformation
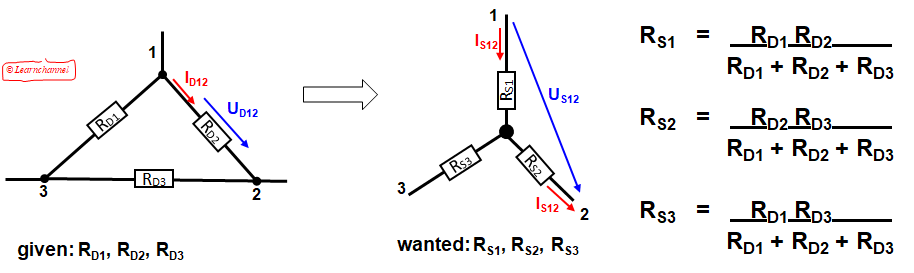
Transformation Delta to Star explained
We proof this:
Condition for the calculation of the resistors RS1, RS2, RS3: Current and voltage values must be the same between the terminals in both circuit types!
We consider the pins 1 and 2:
UD12 = US12 => resulting in RD12 = RS12
ID12 IS12
We consider the pins 2 und 3:
UD23 = US23 => resulting in RD23 = RS23
ID23 IS23
We consider the pins 1 und 3:
UD13 = US13 => resulting in RD13 = RS13
ID13 IS13
Calculation of the resistances between the pins:
RD12 = RD2 ΙΙ (RD1 + RD3) = RD2 (RD1 + RD3) must be equal to RS12 = RS1 + RS2
. RD1 + RD2 + RD3
Resulting in:
RD12 = RD1RD2 + RD2RD3 = RS12 = RS1 + RS2 …Eq.(1)
. RD1 + RD2 + RD3
also:
RD31 = RD1RD2 + RD1RD3 = RS31 = RS3 + RS1 …Eq.(2)
. RD1 + RD2 + RD3
RD23 = RD3RD1 + RD3RD2 = RS23 = RS2 + RS3 …Eq.(3)
. RD1 + RD2 + RD3
We add Eq.(1) + Eq.(2) - Eq.(3):
RD1RD2 + RD2RD3 + RD1RD2 + RD1RD3 - (RD3RD1 + RD3RD2) = RS1 + RS2 + RS1 + RS3 - RS2 - RS3 = 2RS1 . RD1 + RD2 + RD3
We get as a result:
RS1 = RD1 RD2 .
. RD1 + RD2 + RD3
The same way we get:
RS2 = RD2 RD3 .
. RD1 + RD2 + RD3
RS3 = RD1 RD3 .
. RD1 + RD2 + RD3
If the delta connected system has all the same resistance values for RD, then the equivalent star resistors RS will be:
RS = RD RD . = RD .
. RD + RD + RD 3
Star to Delta Transformation
We proceed in the same way for the transformation from star to triangle. The resistors RS1, RS2 and RS3 of the star circuit are converted into the resistors RD1, RD2 and RD3 of the delta circuit with the corresponding resistance values in such a way that the current and voltage values between terminals 1 to 3 are identical.
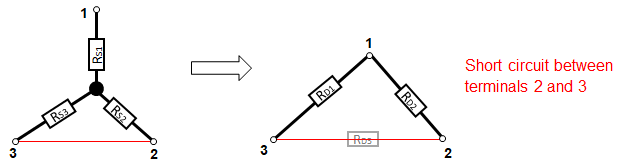
Star to Delta Transformation - how it works
We proof this:
In the star connection, the equivalent resistance between the connection points 1 and 2 (resp.3) is obtained by short-circuiting the connections 2 and 3. Thus, an equivalent conductance is formed from RS1 and the parallel connection of RS2 with RS3.
If the same points are short-circuited in the equivalent delta circuit, the total conductance results from the parallel connection of the resistors RD1 and RD2.

Star to Delta Transformation - how it works
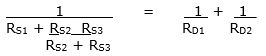
Left side results in a common denominator:
![]()
The same applied to terminal 3 and short-circuited terminals 1 and 2:
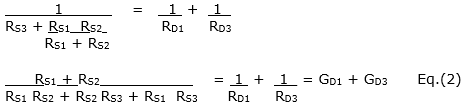
The same applied to terminal 2 and short-circuited terminals 1 and 3:
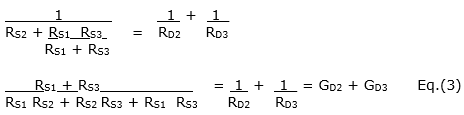
We add: Eq. (1) + Eq. (2) - Eq. (3):
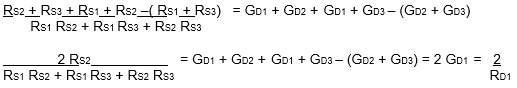
Solve this equation for RD1:
![]()
The same procedure applies to the remaining branches or resistors.
Exercise
Determine the total resistance between the terminals A and B.
R1 = R2 = 10 Ω; R3 = 20 Ω, R4 = R5 = 30 Ω
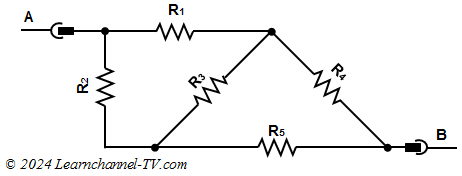
Exercise Star-Triangle transformation
Exercise Star-Triangle transformation Solution RS1 = R3 * R4 / (R3 + R4 + R5) RS2 = R4 * R5 / (R3 + R4 + R5) RS3 = R3 * R5 / (R3 + R4 + R5) R1 + RS1 = 1 0 Ω + 7,5 Ω = 17,5 Ω R1 + RS1 II R2 + RS3 = 8,75 Ω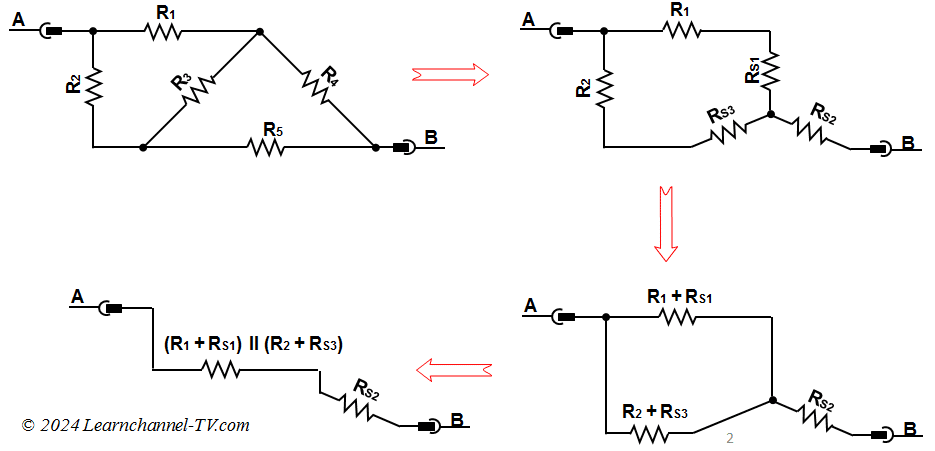
= 20 Ω * 30 Ω / (20 Ω + 30 Ω + 30 Ω)
= 7,5 Ω
= 30 Ω * 30 Ω / (20 Ω + 30 Ω + 30 Ω)
= 1,125 Ω
= 20 Ω * 30 Ω / (20 Ω + 30 Ω + 30 Ω)
= 7,5 Ω
R2 + RS3 = 1 0 Ω + 7,5 Ω = 17,5 Ω
Rges = R1 + RS1 II R2+RS3 + RS2
= 8,75 Ω + 1,125 Ω = 9,875 Ω

