A practical work order without difficult mathematics:

Wheatstone measuring bridge with strain gauge

The final inspection measures the mass m of the filled packages with a strain gauge built within a Wheatstone bridge. The strain gauge has a nominal resistance of R0 = 120 Ω. This changes by +- 10Ω for a change in length of 1μm. The installed strain gauge gets a change in length of 2μm per kg due to load. When the bridge is balanced, the flour package has the correct filling weight.

  1. By how many ohms does the installed strain gauge change its resistance value (ΔR) due to the mass m1 of 1 kg?
  2. What is the mass m2 of the filled package in kg when the bridge is balanced?
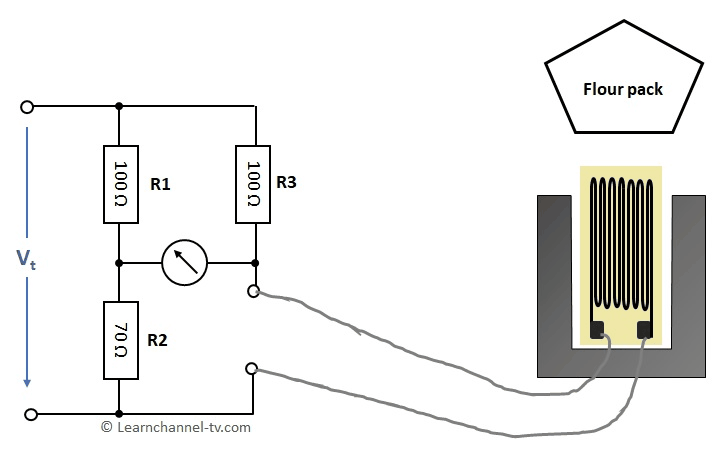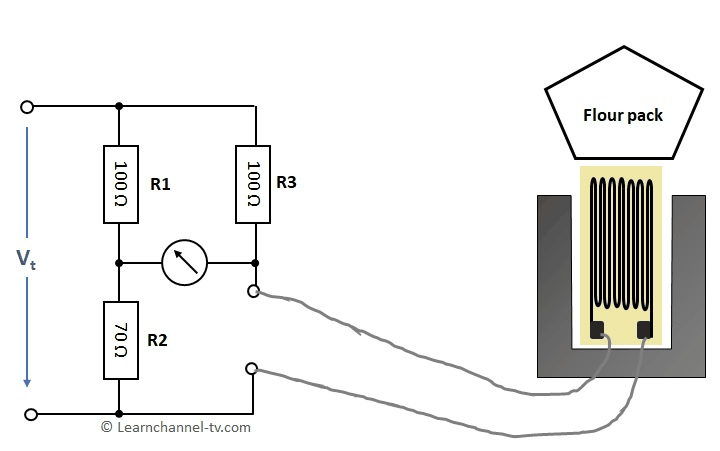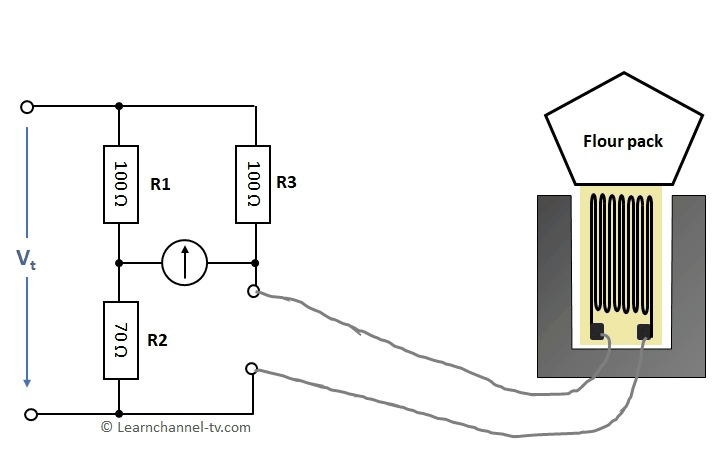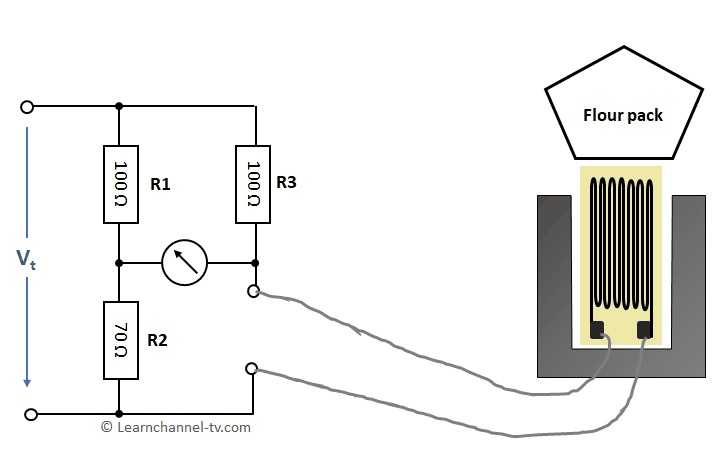
Work order - Calculate a Wheatstone bridge wirh strain gauge

Work order - Calculate a Wheatstone bridge wirh strain gauge