English
Deutsch
Português
Español
- Electrical engineering
- Voltage Current Resistance
- Star Delta Transformation
- Practical Voltage and Current Sources, equivalent circuit diagram
- Capacitor to DC voltage
- Inductors in DC Circuits
- Alternating current
- AC Inductive Circuits
- Three-phase Current
- Transformer
- Complex numbers
- Locus Diagram in AC circuits
- Measurement error
- Videos electrical engineering
- Index electrical engineering
Home ⇒ Overview Courses ⇒ Electrical engineering ⇒ Complex numbers ⇒ Calculating with Complex numbers ⇒ Exercises
Exercises Complex Numbers
- Convert the complex number Z = -4 - j 5 into exponential form.
- Determine the product of the complex numbers Z1= 4 - j and Z2 = 3 + j 4
- The complex number is given in normal form Z = -3 +j 4. Write it down in exponential form.
Regarding task 1: r = √(42 + 52) = 6,4 ¦ φ = arctan(-5/-4) = 51,34° Since the real and imaginary parts are both negative, Z lies in the 3rd quadrant => φ = 180° + arctan(-5/-4) = 231,34 ° Exercises Complex numbers Regarding task 2: First way to solution: Second way to solution: φ1 = arctan(-1/4) = -14,04° => φ = φ1 + φ2 = -14,04° + 53,09° = 39,09° => Z = 20,62 e39,09° Note: Pointer Z1 lies in the 4th quadrant, because real part > 0 and imaginary part < 0, therefore φ1 remains negative and no 180° must be added to it. Test: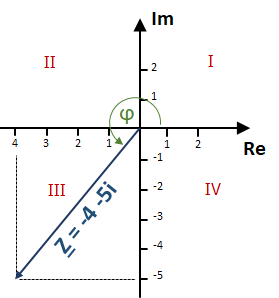
Z = Z1 Z2 = (4 – i)(3 + 4i) = 12 +16i -3i - 4i2 = 16 + 13i
r1 = √(42 + 12) = √17 => r = r1 * r2 = 5√17 = 20,62
r2 = √(32 + 42) = 5
φ2 = arctan(4/3) = 53,09°
Z = 20,62 [cos39,09° + sin39,09°i] = 16 + 13i

