English
Deutsch
Português
Español
- Electrical engineering
- Voltage Current Resistance
- Star Delta Transformation
- Practical Voltage and Current Sources, equivalent circuit diagram
- Capacitor to DC voltage
- Inductors in DC Circuits
- Alternating current
- AC Inductive Circuits
- Three-phase Current
- Transformer
- Complex numbers
- Locus Diagram in AC circuits
- Measurement error
- Videos electrical engineering
- Index electrical engineering
Home ⇒ Overview Courses ⇒ Electrical engineering ⇒ AC Inductive Circuits
AC Inductive Circuits
AC Applied to an Ideal Inductor:
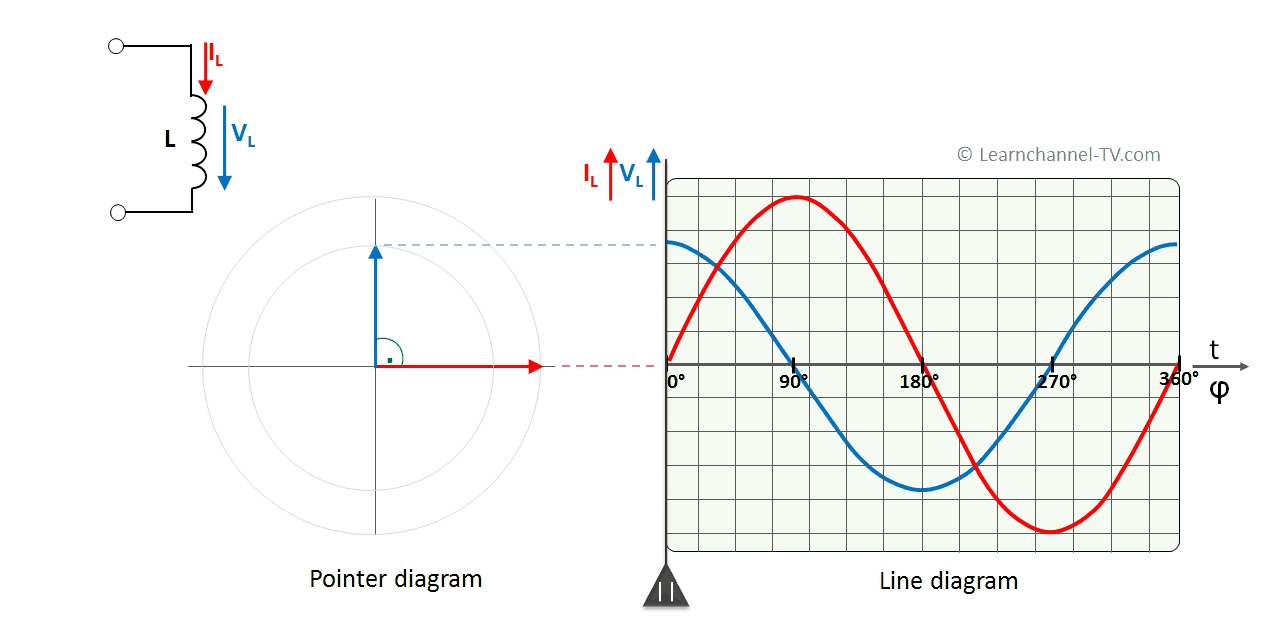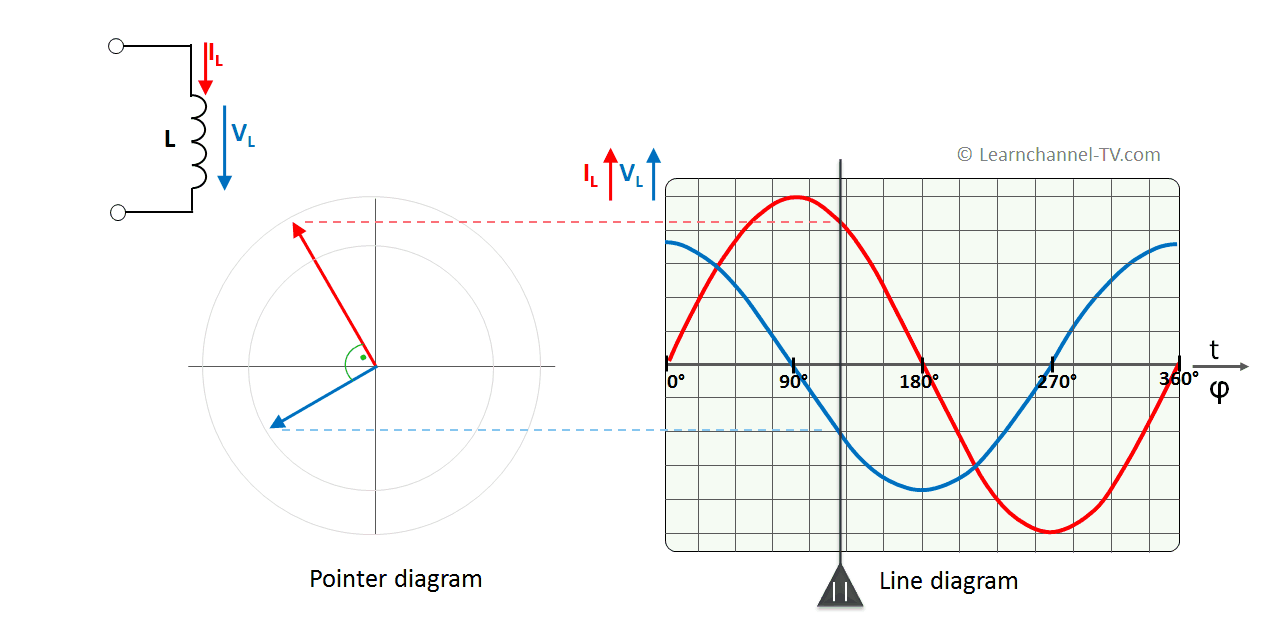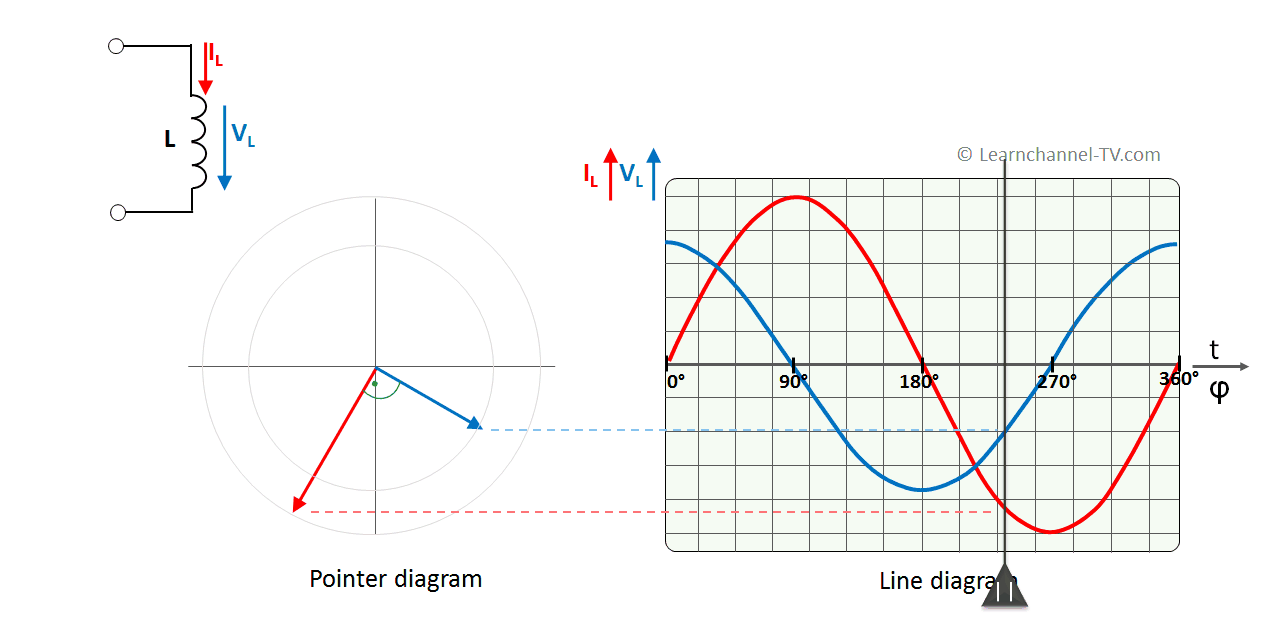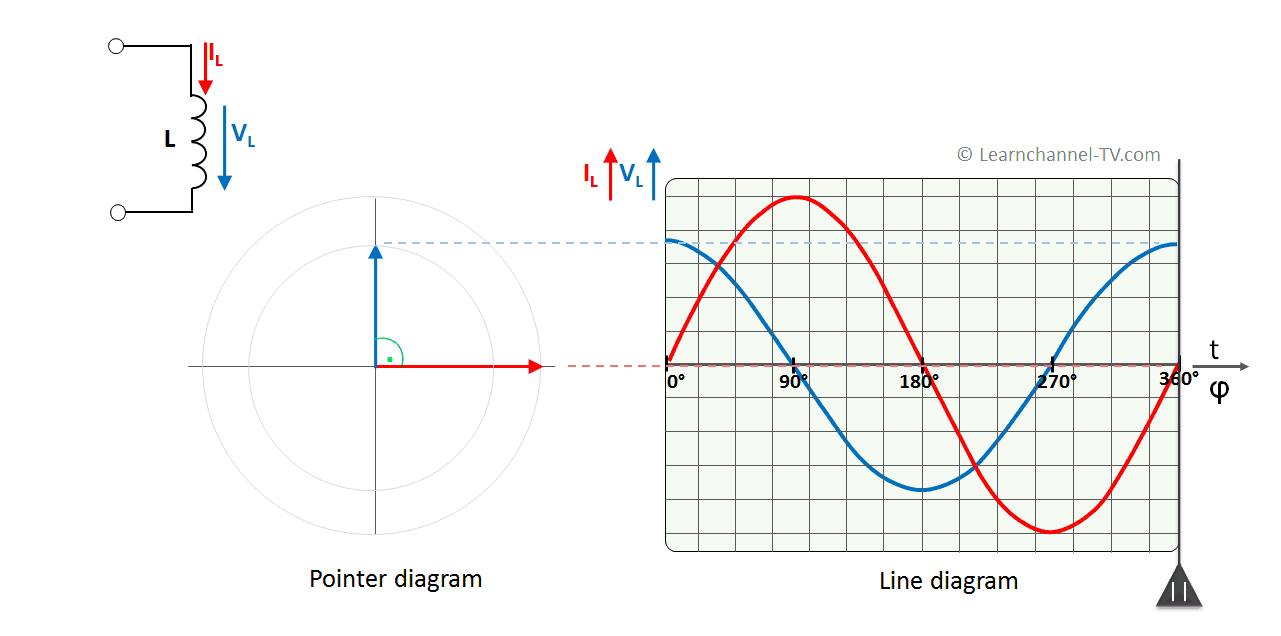
Ideal Inductor to AC voltage - phase shift between current and voltage
As you can see, the current through the coil is 90° out of phase - and delayed. Why?
The periodically alternating current flow creates a magnetic field in the coil that also alternates periodically. This alternating magnetic field in turn results in an induction voltage, which (according to Lenz's rule) is opposite to its cause - namely the applied supply voltage.
With sinusoidal current, the slope or rate of change is maximum at the zero crossing. The self-induction voltage of the coil therefore also must have its maximum at these points.
Conversely, at maximum or minimum of the current curve, the rate of change of the current has the value 0. The value of the self-induction voltage is therefore also 0.
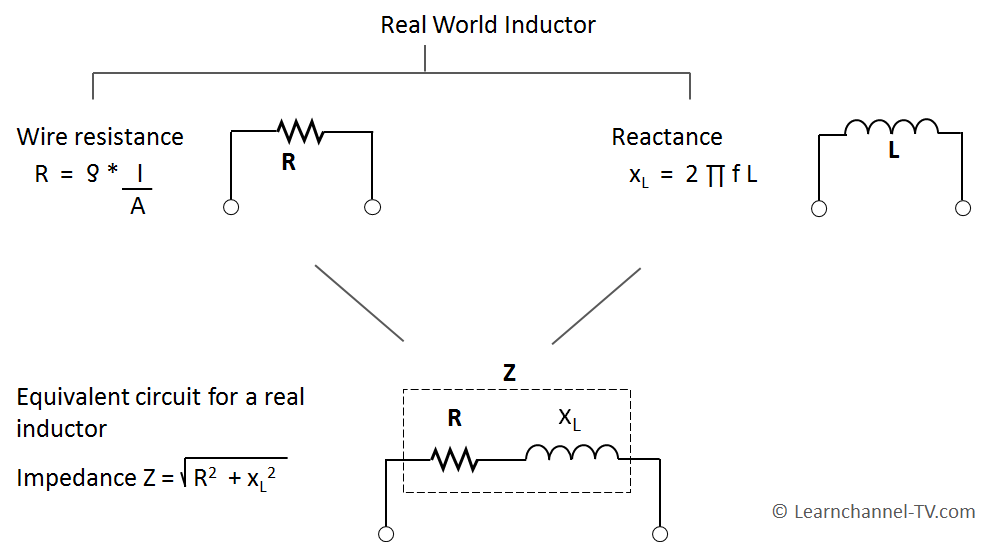
Real World Inductor
Experiment: A real coil is first connected to DC voltage, then to AC voltage. What you see is how at AC voltage the maximum current of 1 A can only be reached with a higher voltage. So an additional resistance has to appear at AC voltage.
You can also see that the current decreases significantly at AC voltage supply as soon as you insert an iron core. At DC voltage supply this has no influence.
Every real world inductor has some unwanted wire-resistance. So the total resistance, called Impedance is a combination of the wire-resistance and the reactance:
What is the difference between a real-world inductor and an ideal inductor?
The ideal inductor has only an inductive reactance (XL = 2 π f L). With the real-world inductor, the wire resistance is taken into account.
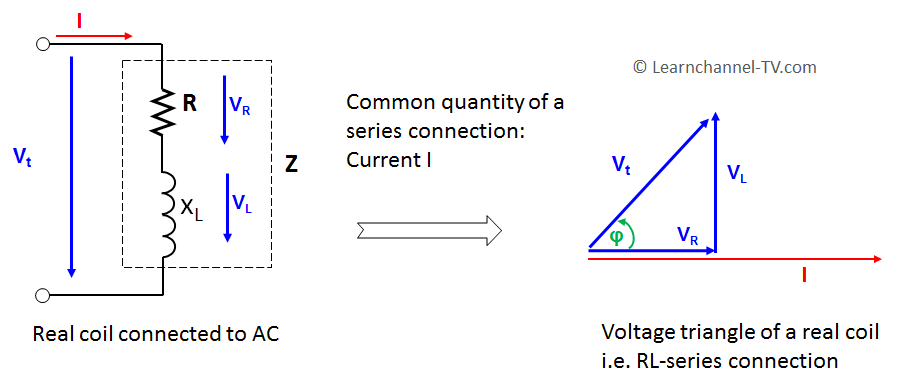
In the equivalent circuit diagram of a real coil ohmic resistance and reactance are in series. Nevertheless, the total resistance or impedance is determined by means of Pythagoras. The Pythagoras can be applied to right-angled triangles. This resistance triangle, like the power triangle, can be derived from the voltage triangle:
If the current I is the common value of a series connection, each side of the voltage triangle can be multiplied or divided by the current I. This results in 2 equiangular triangles: