Father drives his car at a speed v1 of 100 miles/h. The son sets off on his motorbike half an hour later at a speed v2 of 150 miles/h. When and after what distance did the son catch up with his father?
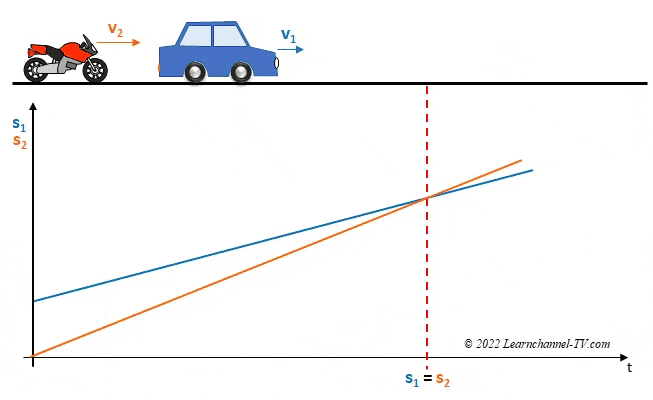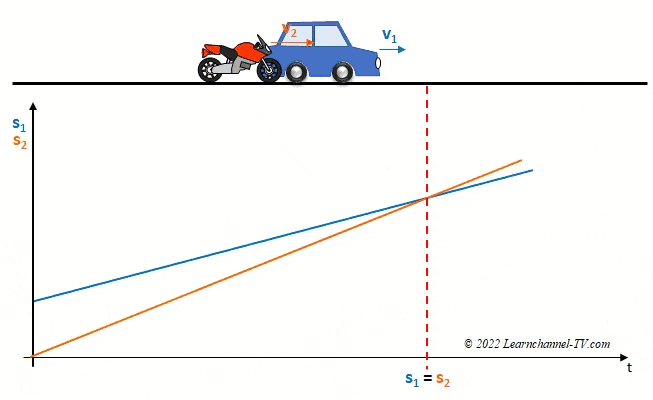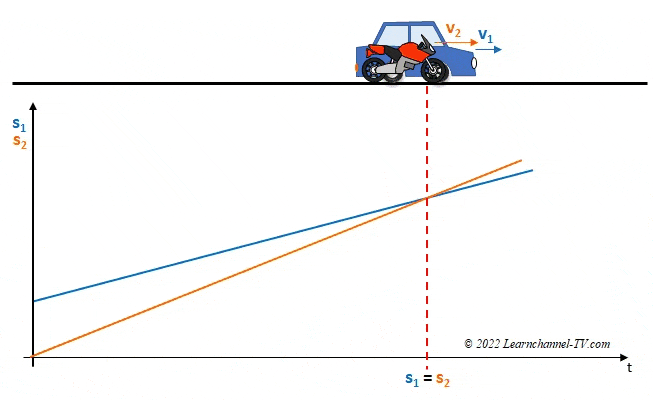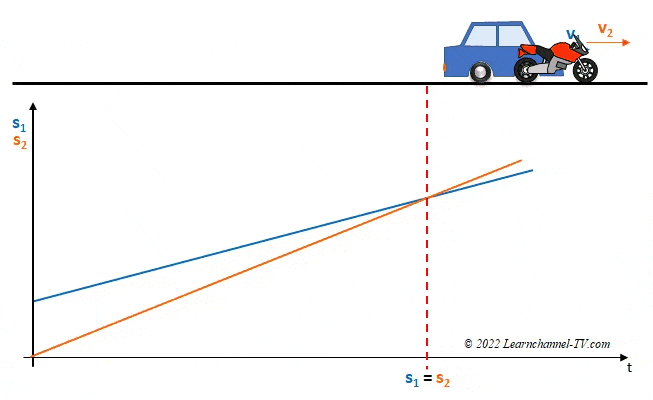
Exercise - Motion with constant speed
Exercise 2:
Father starts with his car at a speed of 100 miles/h from place B. At the same time, his son starts with his motorcycle from place A to meet his father. His speed is 150 miles/h. At which point do they meet if the two places are 100 miles apart?
When the motorcycle catches up with the car, both have covered the same distances at this point, i.e. the condition is: ∆s1 = ∆s2
Until the motorcycle starts after ∆t = 0.5 h, the car with v1 = 100 miles/h has a lead of: 100 miles/h × 0.5 h = 50 miles. The following must therefore apply to the meeting point:
∆s1 = ∆s2 => v2 × ∆t = 50 miles +v1 × ∆t
∆t is the time that passes from the start of the motorcycle. Solving the equation for ∆t:
v2 × ∆t – v1 × ∆t = 50 miles => (v2 – v1)∆t = 50 miles => ∆t = 50 miles / (150 mph - 100 mph) = 1h
The distance is easy to calculate. We consider the motorcycle:
∆s = 150 miles/h × 1h = 150 miles
Exercise 2
We choose location A as the coordinate origin (reference point) and designate the direction of travel from A to B as positive. The speed of the car is evaluated negatively, because it runs in the opposite direction.
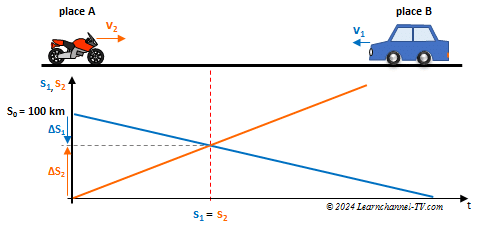
Physics - Linear Motion with constant speed - exercise 2
Thus, the location functions for both vehicles are:
s2 = v2 × t and s1 = s0 - v1 × t
Cond. for meeting point: t1 = t2 = t
⇒ v2 × t = s0 - v1 × t ⇒ t(v1+v2) = s0 ⇒ t = s0 / (v1 + v2) ⇒ t = 0.4 h
Thus, both vehicles meet after 0.4 h. To dermine the distances, that both vehicles have at this time from the coordinate origin (location A), we take the simpler equation for s2:
