OP-Amp as Non-Inverting Amplifier

OP Amp as Non-Inverting Amplifier

Here the output signal is fed back to the inverting input by a voltage divider. The output signal is divided by the voltage divider, which results in an output signal being amplified. The resistance ratio determines the gain factor.

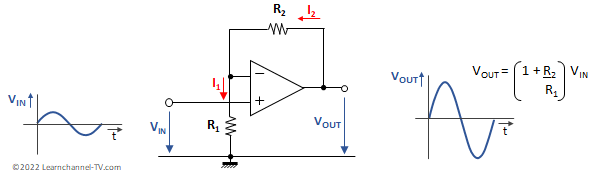
Non-Inverting Operational Amplifier - Non-Inverting Op Amp

Since the input resistance of an operational amplifier is very high, the input currents are negligible. Thus: I₁ = I₂  (1)

Since the differential voltage at the inputs of the operational amplifier is zero, the following applies: V_R1 = V_IN      (2)

Apply the mesh rule and you get for the output voltage V_OUT:

V_OUT = V_R1 + V_R2   or    V_OUT = V_IN + V_R2

With I₁ = I₂ and Ohm's law you get:

Exercise - OP-Amp as Non-Inverting Amplifier

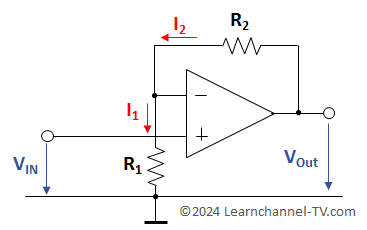
Op-Amp as Non-Inverting Comparator - exercise

Exercise 1:

Calculate the output voltage with the following values: R₁ = 2 kΩ, R₂ = 22 kΩ, V_IN = - 500 mV

Exercise 2:

R₁ = 2 kΩ,   R₂ = 22 kΩ,  U_e = 1 V

1. What voltage is measured between the inverting and the non-inverting input in the steady state ?
2. Calculate the current flowing through R₂ ?
3. What is the voltage drop across R₂?