English
Deutsch
Português
Español
- Closed Loop Controls
Home ⇒ Overview Courses ⇒ Closed Loop Controls ⇒ Analog controller
Analog controllers or Controllers PID
Examples of analog controls: speed control, positioning control, torque control, voltage control, etc. What do all these controls have in common? They control a fast reacting system!
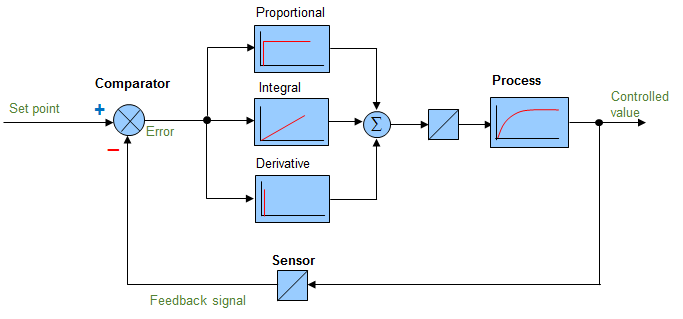
Block diagram of a PID control
Let us explain the function of a PID controller in this video:
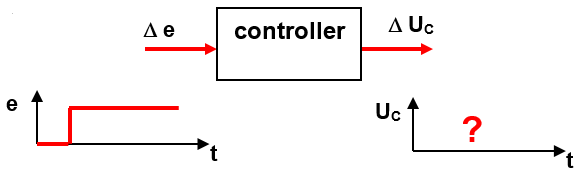
step response controller
Analyze the control behavior
Principle: A voltage jump of ideally 1V is applied to the input of the controller. The parameters of the controller are determined by means of the step response. We regard the P, I and D shares on their own:
.
P-controller or proportional controller
A P-controller has an output signal u(t), that is proportional to the control error (u ~ e) without delay. As soon as the control error returns to the value 0, this controller does not have an output signal u any more.

step response P-controller
Determine the parameter proportional gain factor Kp: Kp = Δ u / Δe
Although a P-controller reacts immediately, a pure P-control has a permanent control deviation!
I-Controller or Integral-controller
The integral part is used for optimization because it can reduce a control deviation to zero. As you can see, the Integral force increases steadily as long as there is still a control deviation. When the control deviation is zero, the I-force remains at its constant value and reduces again only by a control deviation with opposite sign.

step response Integral-controller
Determine of the parameters for the I-force:
Since the output signal of the I-force constantly changes during a control deviation, you would relate the slope of the I-force to the input quantity e:
Integral gain KI : KI = (Δ u / Δt) / Δ e = (u – u0) / (Δt * Δe)
The unit of this integral gain KI is 1/s. Because this parameter is hard to understand for the user you would use the so-called Integral time, which represents the reciprocal:
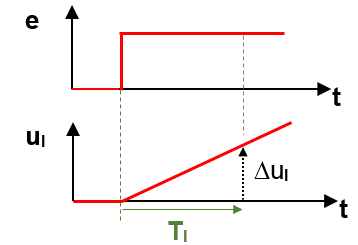
Integral-time I-controller
Integral time TI = 1 / KI = (Δ t * Δe ) / Δu (without regarding the sign)
.
To tell it in a few words: TI is the time until the output equals the level of the input signal.
.
.
D-controller or Differential controller
The differential-part also serves for optimization. With its force, the controller reacts to a change of a control deviation very quickly. It also dampens the oscillation of the control.

step response D-controller
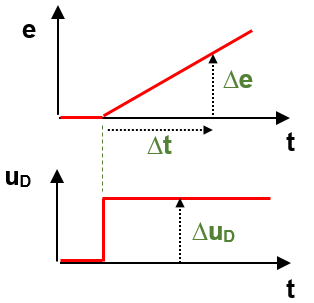
Determine parameter of a D-controller
The D controller reacts to a change in the control deviation! Problem: No parameters can be derived from the step response of a D controller. Trick: As input signal we use a ramp:
Derivative gain KD
KD = Δ u _ _ = Δ u * Δt
. Δ e / Δt Δe..
.
.
Exercises - Controller in automation:
Multiple Choice:
![]()
Step response of a PI-Controller
Empirically, you have set the PID controller as best as possible with the following parameters: KP = 1.5, Ti = 0.002 s
A voltage jump of 1 volt is applied to the input of the controller. Complete the step response of the P- and I-force as well as the combined PI controller on the solution sheet.
Exercise Step-response PI-controller
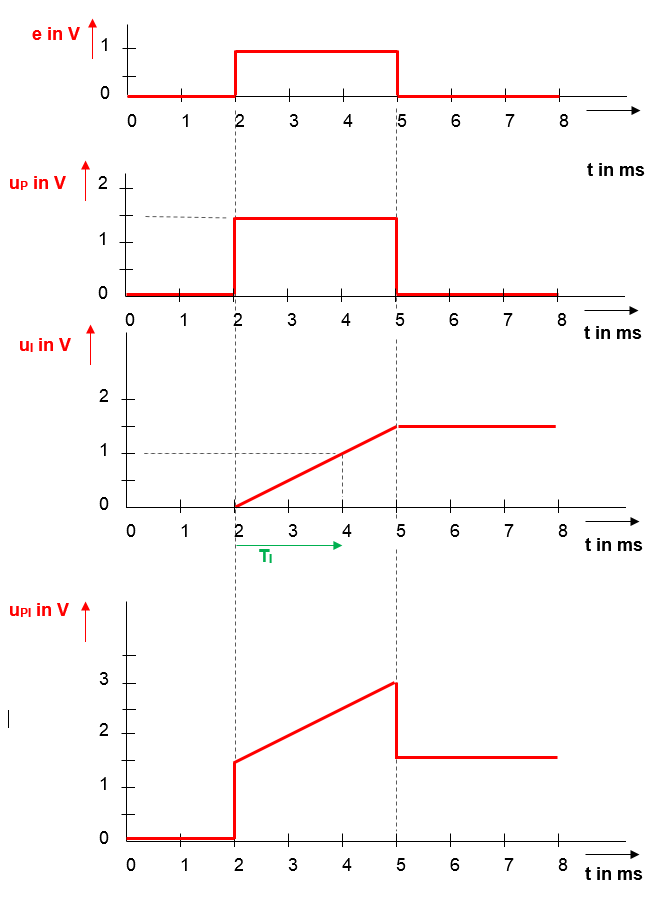
Step-response PI-controller - solution

