English
Deutsch
Português
Español
- PLC Programable Logic Control
- What is a PLC
- Analog and Digital
- PLC Programming Languages
- Basic Logic Functions
- Combinatorial Logic
- Wire Break Detection
- Algebraic Simplification of Logic Circuits
- Karnaugh map
- PLC Exercises I
- PLC-exercises II – boolean algebra
- PLC exercise – Tank level monitoring
- Work Order PLC Material detection
- How a PLC works
- PLC function Set and Reset
- PLC-Program for H-Bridge
- Sequence control
- Analog value processing
- Bus Network
- Number Systems
- Videos about PLC
- Index PLC
Home ⇒ Overview Courses ⇒ PLC ⇒ Simplification of Logic Circuits
Simplifying logical circuits
Do you take many circuits too complex? If do so, then you can simplify them.
Simplifying by using Boolean algebra
The following rules apply for variables which are used in logical functions. The analogy to the electrical circuit should help you to work out these rules for yourself:
First part: Signal a combined with a constant:
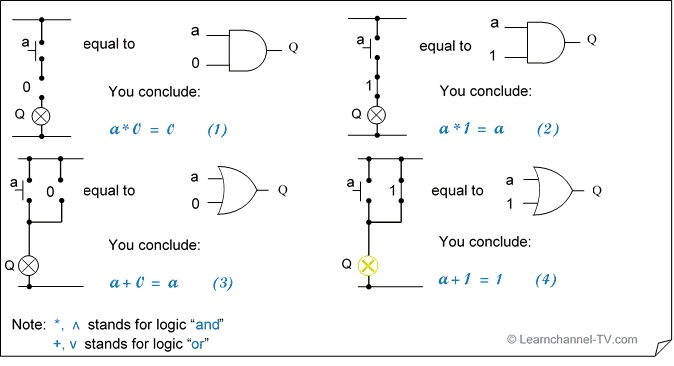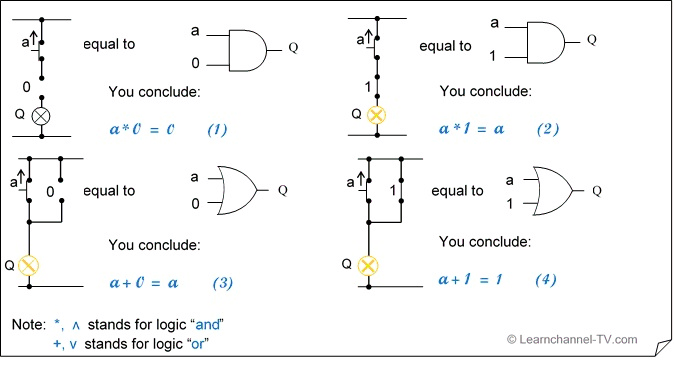
Simplifying by using Boolean algebra 1
Second part: Variable combined with itsself
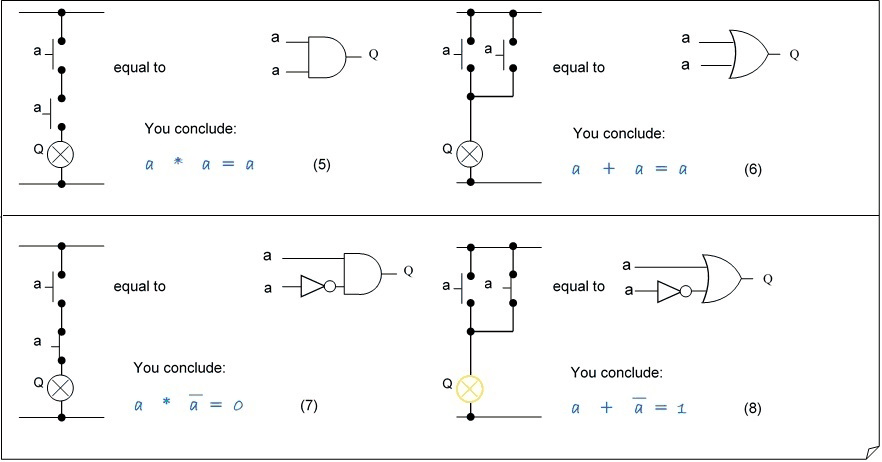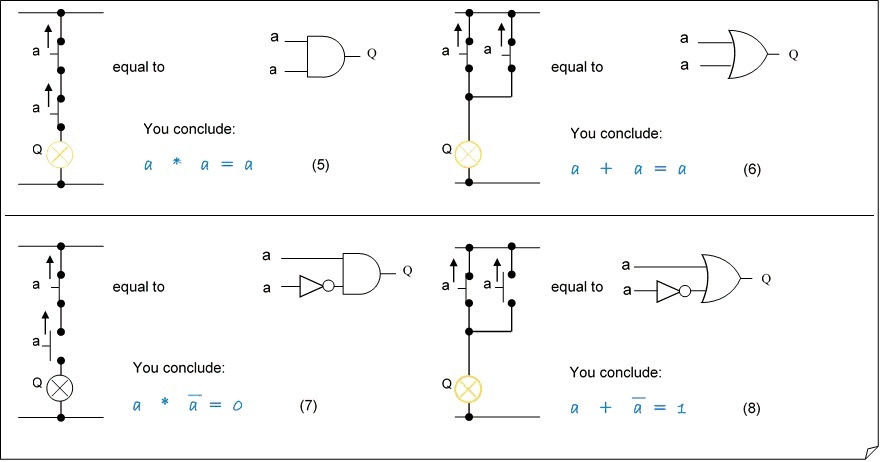
Simplifying by using Boolean algebra - Variable combined with itself
Third part: Commutative law
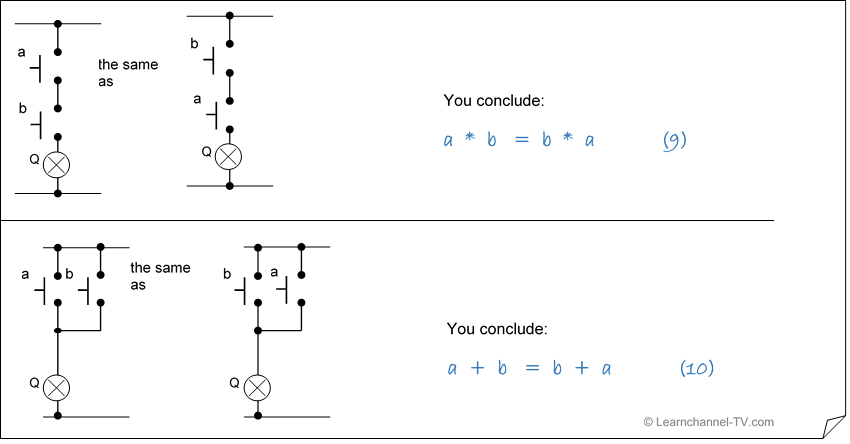
Simplifying by using Boolean algebra - the Commutative law
Fourth part: Associative rule
The associative rule tells you how you can summarize single variables, which are linked to each other by, AND 'or' OR '. Summarized variables are indicated by parentheses.
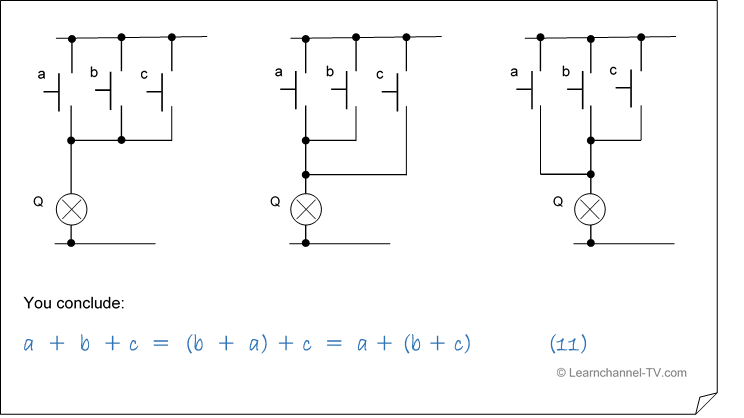
Simplifying by using Boolean algebra - Associative rule
Fifth part: Distributive laws
The Distributive laws specify how links relate to each other when parentheses are resolved (Law of distribution for calculating with parentheses).
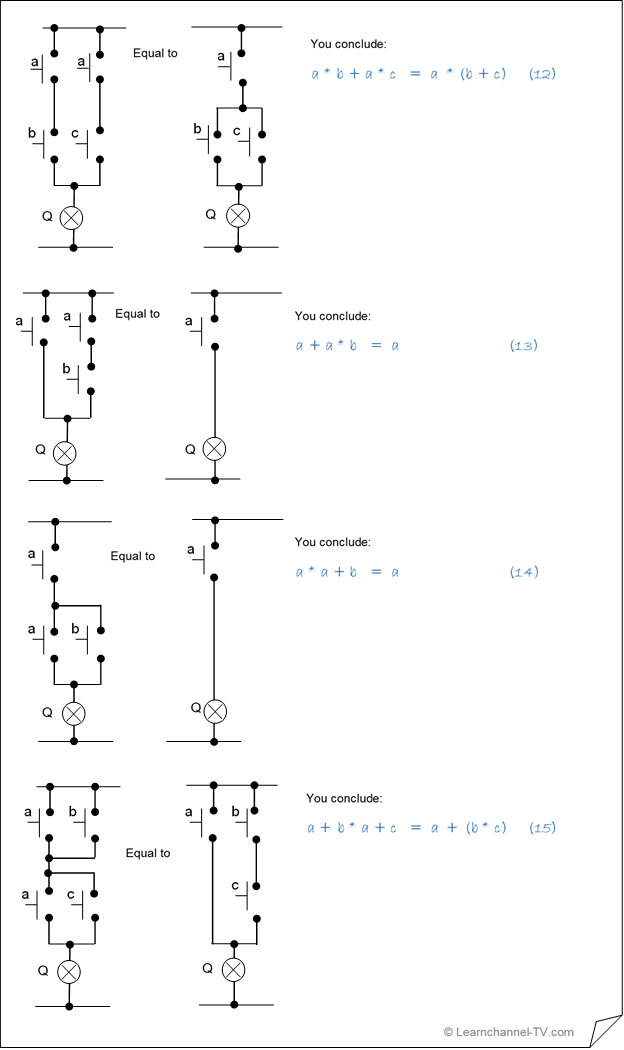
Simplifying by Boolean algebra - the Distributive laws
Sixth part: The rule of “de Morgan”
The De Morgan's rules are used to transform logic circuits.
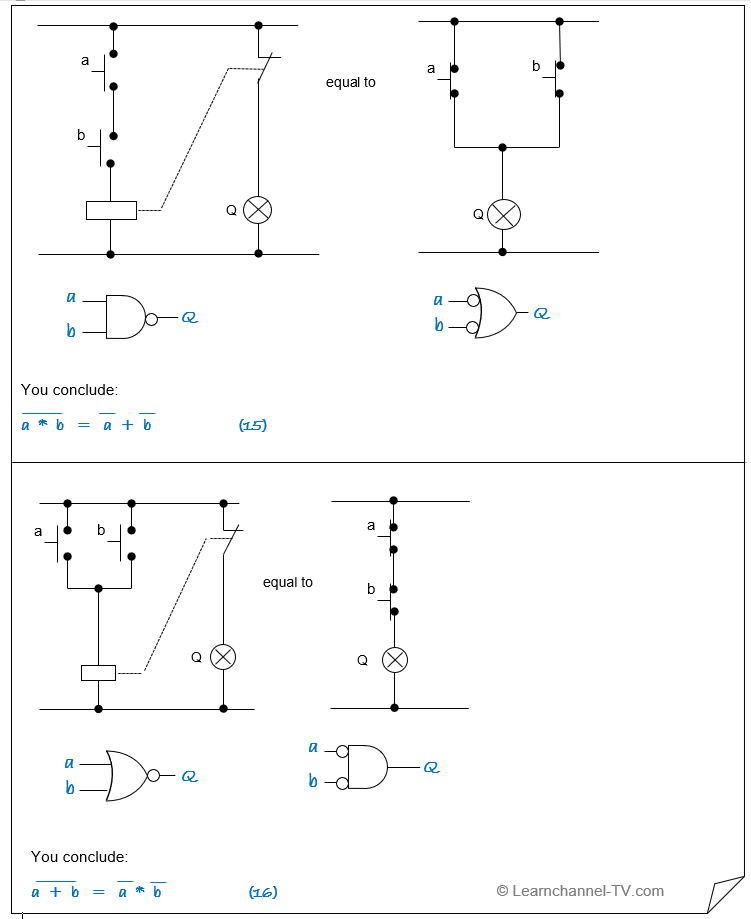
Simplifying by using Boolean algebra - De Morgan's law

