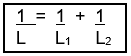English
Deutsch
Português
Español
- Electrical engineering
- Voltage Current Resistance
- Star Delta Transformation
- Practical Voltage and Current Sources, equivalent circuit diagram
- Capacitor to DC voltage
- Inductors in DC Circuits
- Alternating current
- AC Inductive Circuits
- Three-phase Current
- Transformer
- Complex numbers
- Locus Diagram in AC circuits
- Measurement error
- Videos electrical engineering
- Index electrical engineering
Home ⇒ Overview Courses ⇒ Electrical engineering ⇒ Inductors in DC Circuits ⇒ Inductors in Series and Parallel
Inductors in Series
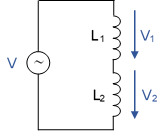
Inductors in Series
We consider two coils connected in series, which are connected to AC voltage.
According to the rules of series connection:
V = V1 + V2 Eq. (1)
We remember: Due to the law of self-induction, the voltage U caused on the coil (due to the change in time that we just have with AC voltage) can be written as follows:
![]()
Eq. (2) in Eq. (1) and you get:
![]()
Note: The minus sign has been shortened. According to the rules of series connection we have only "one" current. By further shortening it follows:
![]()
Inductors in Parallel
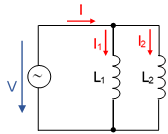
Inductors in Parallel
According to the rules of parallel connection applies:
I = I1 + I2 Eq. (3)
Since we are considering here the behavior of inductors at AC voltage, we form the differentiation of Eq. (4):
dI = dI1 + dI2 Eq. (5)
dt dt dt
from V = - L dI it follows dI = - V Eq. (6)
. dt dt L
Eq. (6) in Eq. (5), the minus sign is shortened. You get:
V = V + V
L L1 L2
According to the rules of parallel connection, we have only one voltage. Thus follows: