English
Deutsch
Português
Español
- Electrical engineering
- Voltage Current Resistance
- Star Delta Transformation
- Practical Voltage and Current Sources, equivalent circuit diagram
- Capacitor to DC voltage
- Inductors in DC Circuits
- Alternating current
- AC Inductive Circuits
- Three-phase Current
- Transformer
- Complex numbers
- Locus Diagram in AC circuits
- Measurement error
- Videos electrical engineering
- Index electrical engineering
Home ⇒ Overview Courses ⇒ Electrical engineering ⇒ Complex numbers
Complex numbers are mainly used in electrical engineering. Just think of the phase shift of inductive and capacitive loads or the calculation of complex resistances. So let´s take the first steps together to understand these complex numbers.
Overview - Number sets in mathematics
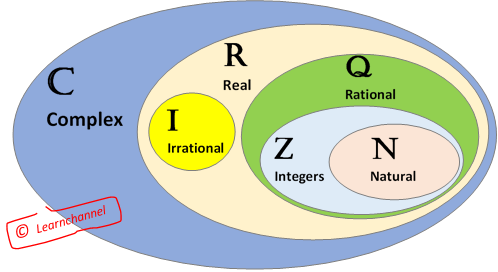
Number sets in mathematics
The numbers you can make by dividing one integer by another are named as Rational Numbers Q (Q stands for "quotient"). In other words, fractions.
Examples: 5/2 (= 2.5), 10/5 (= 2), -3/100 (= -0.3)
An Irrational Number is a real number that cannot be written as a simple fraction.
Example: π= 3,1415…, Euler`s number e = 2,71828... , √2 = 1,41421...

Difference between rational and irrational number
Natural Numbers can mean either "Counting Numbers" {1, 2, 3, ...}, or "Whole Numbers" {0, 1, 2, 3, ...}, depending on the subject.
Integers are like whole numbers, but they also include the negative numbers. Zero is also included.

Definition Integer
A complex number exist of a real part and an imaginary part:
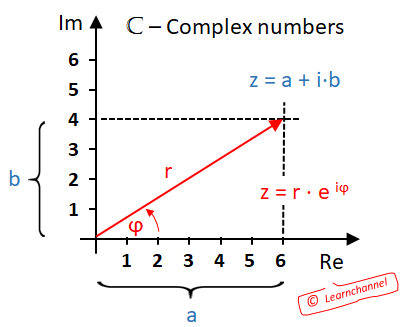
Complex numbers - Complex Plane
A complex number exist of a real part and an imaginary part. You can describe a complex number as:
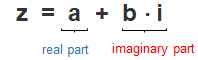
Defing a Complex number
As you can see, all real numbers are also complex numbers with an imaginary part of zero.
This type of representation is referred to as algebraic form. Another possibility of representation is the trigonometric form and derived from it the Eulers formula. This is where the pointer length and angle are specified:
z = r × e iφ

