English
Deutsch
Português
Español
- Electrical engineering
- Voltage Current Resistance
- Star Delta Transformation
- Practical Voltage and Current Sources, equivalent circuit diagram
- Capacitor to DC voltage
- Inductors in DC Circuits
- Alternating current
- AC Inductive Circuits
- Three-phase Current
- Transformer
- Complex numbers
- Locus Diagram in AC circuits
- Measurement error
- Videos electrical engineering
- Index electrical engineering
Home ⇒ Overview Courses ⇒ Electrical engineering ⇒ Capacitor to DC voltage
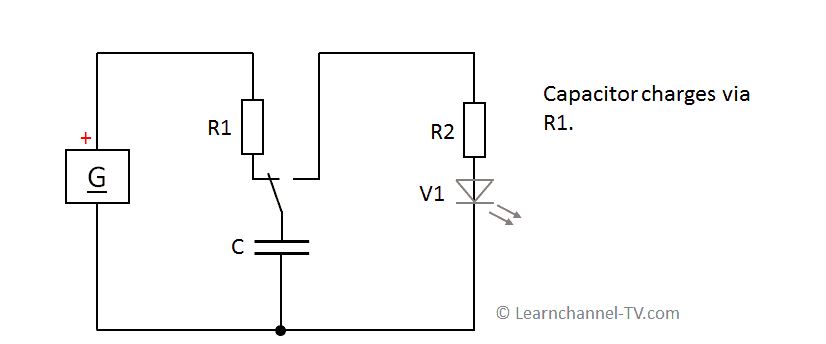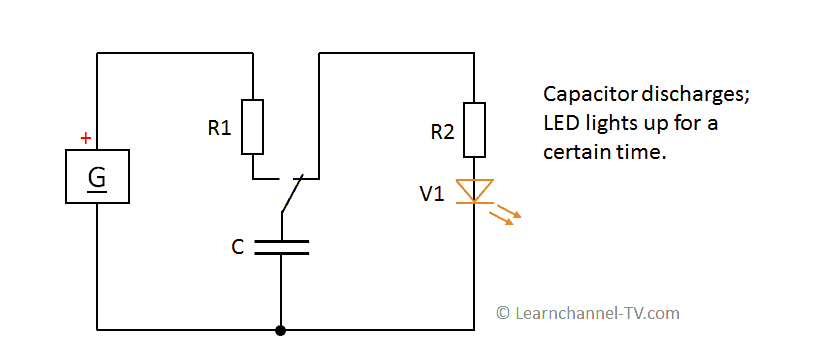
The capacitor on DC voltage - an energy store
Test:
Here is the circuit diagram for a better understanding:
Energy Stored on a Capacitor
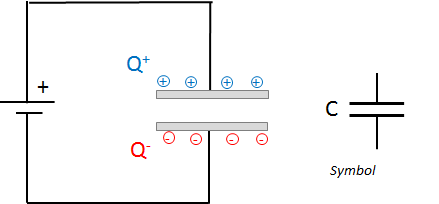
Capacitor - Function and Symbol
At DC voltage, the capacitor acts as a charge accumulator. Essentially, the capacitor consists of two plates, which are electrically separated from each other - either by air or by an insulator (dielectric).
A characteristic value of the capacitor is the capacitance C. It describes the capacity of the capacitor to store a certain amount of charge Q on its plates at a certain voltage.
Q = C * V or C = Q / V
Colloquially expressed: "The larger the capacitor and the higher the voltage, the more charges find room on the capacitor plates".
Unit: [C] = Farad F = 1 C / V ("One Farad equals one Colomb per Volt")
Usual sizes:
Millifarad mF = 10-3 F
Microfarad µF = 10-6 F
Nanofarad nF = 10-9 F
Picofarad pF = 10-12 F
How to determine the capacity of a capacitor?
Plate distance: The smaller the plate distance, the more the charges on the opposite plate attract each other and the "more" charges therefore find "space" on the plates.
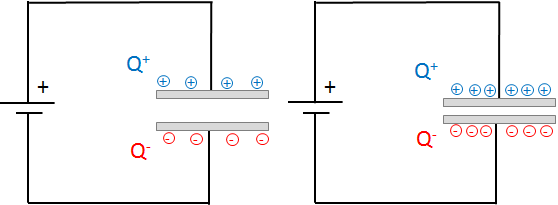
Capacitor - Plate distance and capacity
Plate area A: The larger the plate areas, the more loads can be stored on the plate.
Dielectric: Electric dipoles of the dielectric align themselves with the charges of the capacitor and "neutralize" them. Thus, more charges find place on the plates of the capacitor.
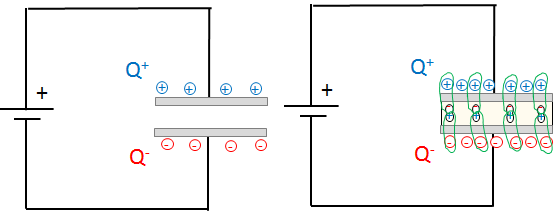
Capacitor - Dielectric and Capacity
Charge- and Discharge Curve
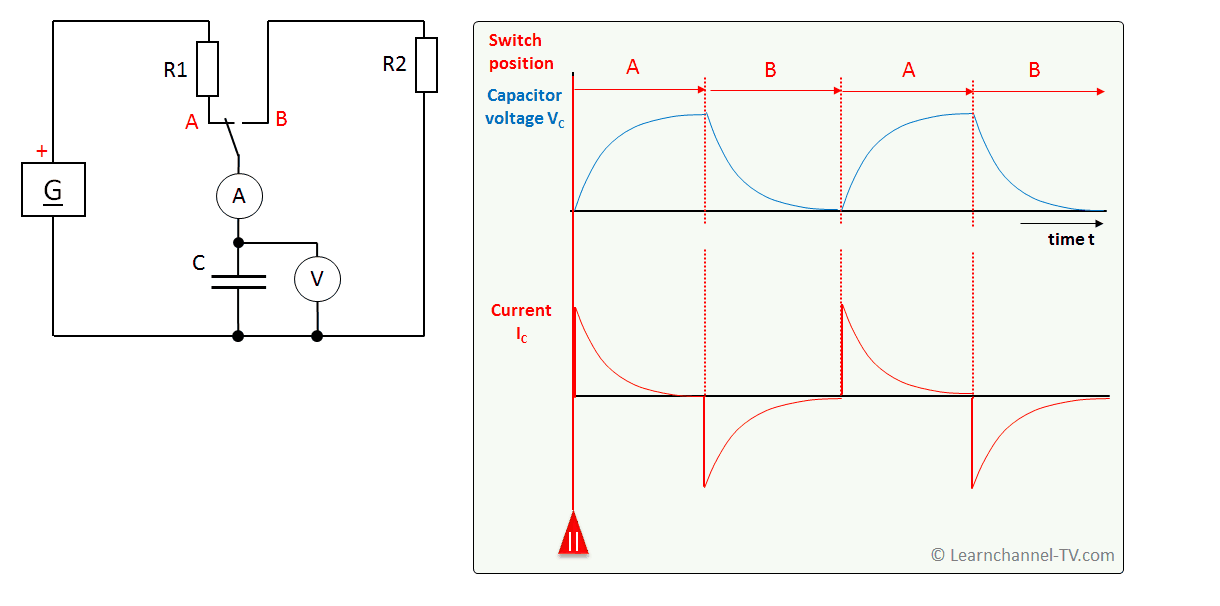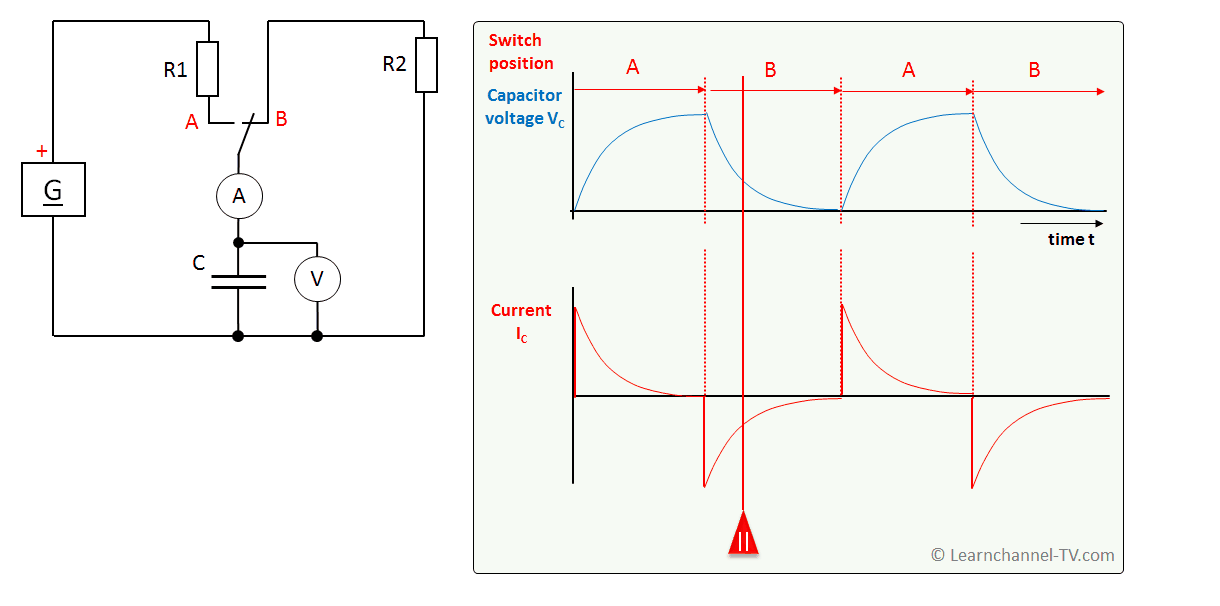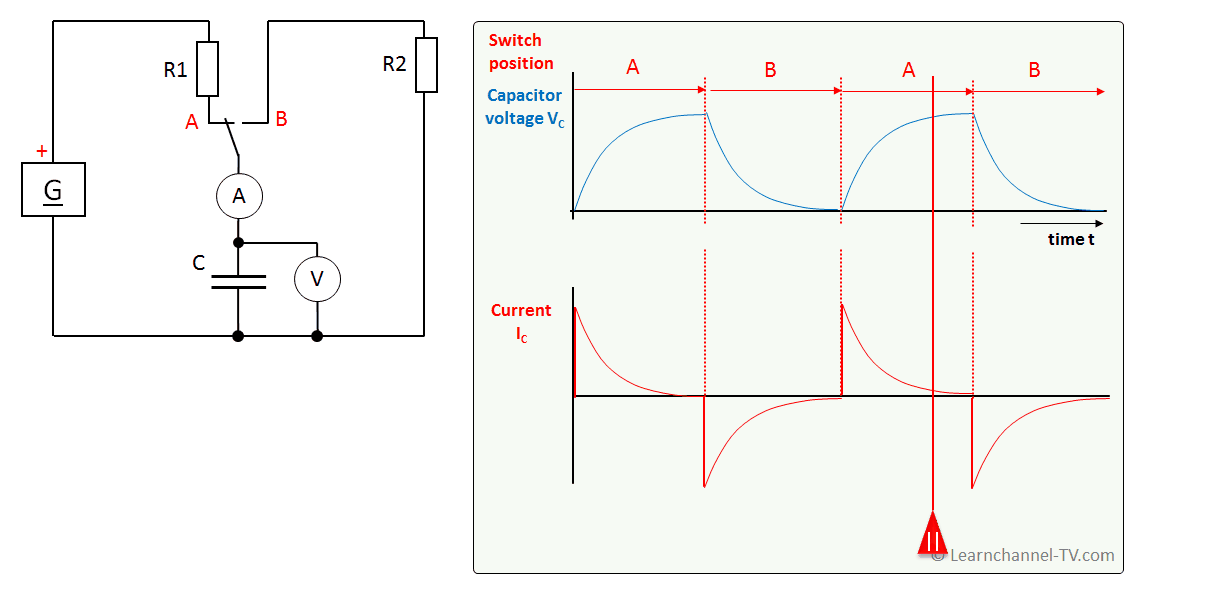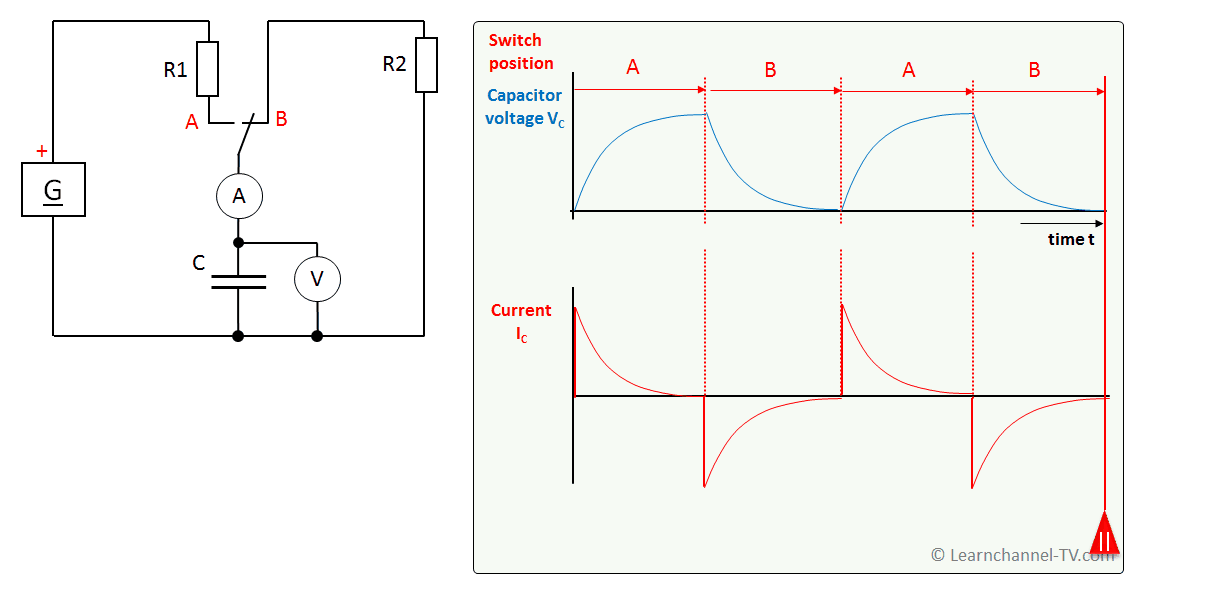
Capacitor - Charge- and Discharge curve
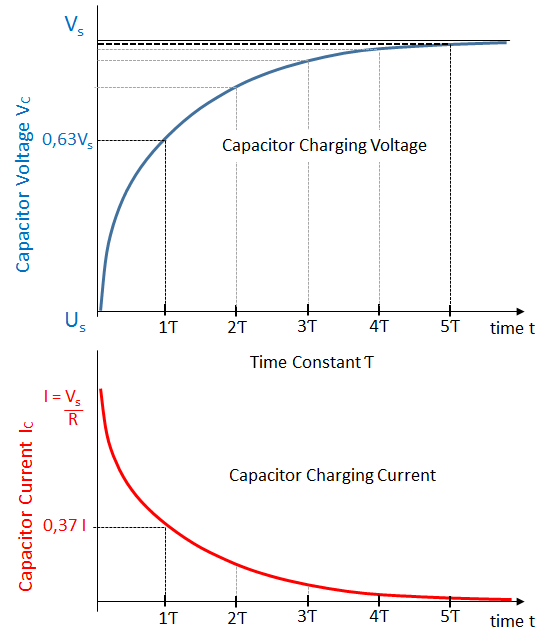
Capacitor Charging Graph
Determine the time to charge or discharge a capacitor
As can be seen, the charge and discharge curves of a capacitor have a curvilinear shape, which can be described according to an e-function. Therewith, the capacitor would actually never be fully charged, a thing that of course does not make sense in practice.
In general, a capacitor charges and discharges more slowly the larger its capacity and the larger the resistor R in series. This is the basis for the so-called Time constant Ƭ (pronounced "Tau"):
Ƭ = R * C in seconds s
In practice, you would apply the following rule of thumb: The capacitor is fully charged or discharged after 5 Ƭ. The capacitor voltage has thus reached 0.99 of the supply voltage.
The level of the applied voltage has no influence on the charging time!
Always charge and discharge capacitors - especially larger ones - via a series resistor!

